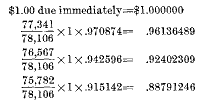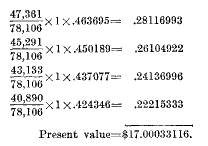Computation of the Net Annual Level Premium

1. Term Insurance. In computing net annual level premiums it is first necessary to ascertain the net single premium. This has been done in Chapters XIII and XIV for the more usual types of policies. The second step will be to define carefully the premium-paying period over which the annual premium is to be paid and for which the life annuity due is to be ascertained. Suppose it is desired, therefore, to compute the net annual level premium which will purchase a five-year term insurance of $1,000 at age 45, American Experience 3 percent, basis. It was found on page 154 that the net single premium on this policy was $53.86. Beginning at date of issue the annual premium will be paid over a five-year period, or until prior death, and is therefore a five-year term annuity due.

Since the amount of the annual premium is the unknown quantity it will be impossible to proceed directly to the computation of its present value, but it is feasible to take any assumed premium, such as $1.00, and compute the present value of an annuity due for this amount. An annuity due of $1.00 on the policy in question will be equal to a term annuity for four years plus $1.00 paid immediately and its present value is computed in the following manner:

The present value of a five-year term annuity due of $1.00 at age 45 is, therefore, equal to $4.6124 and the annuity due, or annual premium, of $1.00 for this period will purchase any policy the present value, or net single premium, of which is equal to $4.6124. But the net single premium on the policy in question was found to be $53.86. If now the present value of the $1.00 annuity due be divided into the net single premium on this policy the resultant factor will show how many times the annual premium of $1.00 must be taken to, obtain an annual premium the present value of which will equal the net single premium, or $53.86. Stated in other words, the annual premium desired is as many times $1.00 as the net single premium on the policy is times the present value of a $1.00 annuity due for the premium-paying period. From this analysis it is possible to state a general rule for ascertaining the net annual level premium on any policy as follows: Divide the net single premium by the present value of a life annuity due of $1.00 for the premium-paying period. Performing this computation, it is found that the net annual level premium on a five-year term insurance of $1,000 issued at age 45 is $11.68, thus:

53.8600/4.6124 = $11.68.

2. Ordinary life insurance. The net single premium for a whole-life policy of $1,000 issued at age 45 is $504.59 according to the figures on page 157. To find the net annual level premium this sum must be divided by the present value of a life annuity due for the whole of life, since premiums are paid continuously through the life of this policy. The method of ascertaining the present value of the life annuity due of $1.00 follows herewith:

If, therefore, $17.0093 is the present value of a life annuity due of $1.00, it is possible for an annual premium of $1.00 paid continuously throughout life to purchase any whole-life policy the present value, or net single premium of which is $17.0093; and the net annual level premium necessary to purchase a life policy for $1,000 will be found, according to our formula, by dividing this sum into $504.59, the net single premium, as shown herewith:

504.5900/17.9098 = $29-67 net annual level premium.

The net annual level premium for an ordinary life policy of $1,000 issued at age 45, American Experience, 3 percent, basis, is therefore $29.67.

3. Limited-payment life policy. If it is desired to pay for the above whole-life policy In twenty annual payments instead of allowing them to continue throughout life, it is required to compute the annual premium, which, continued for twenty years, or ceasing upon prior death, will purchase this policy. In accordance with our formula the annual premium in this case will be found by dividing into the net single premium the present value of a temporary life annuity due for a term of twenty years following age 45. If from the life annuity due computed on page 180 heretofore, the sum of the first twenty terms be taken, this amount will equal the present value of a twenty-year term annuity due. This is found to be $13.5095. The net annual premium therefore for a twenty-payment life policy at age 45 is 504.59/13.5095 or $37.35.

4. Deferred annuity. Deferred annuities are ordinarily paid for by means of annual rather than single premiums, and the premium may continue through the entire period of deferment or, as in the case of the whole-life policy above, may be limited to a stated number of years. As with premiums on insurances, the annual premium on these contracts is paid only during survival. If, therefore, the deferred annuity issued at age 40 begins the payment of an annual income of $100 at age 70 if living, and if the net single premium for it is $155.947 as determined on page 170, the continuous annual premium on this policy may be paid until one year prior to the beginning of the annuity, or until the holder of the contract is aged 69. In this case the annual premium becomes a temporary annuity due for a term of thirty years, ages 40 to 69 inclusive. The amount of this net annual premium will be found therefore by dividing the net single premium by the present value of an annuity due of $1.00 computed for the term stated. This annuity value is computed as follows:

The result obtained represents the present value of an annual premium of $1.00 paid over the same term as the premiums on the deferred annuity and this figure divided into the net single premium for the deferred annuity will give a net annual level premium of $9.173 -|~, as follows:

155.947/17.5003 = 9.173.

The annual level premiums computed to this point should afford a sufficiently clear analysis of the subject of the level premium. The principles thus developed can be applied in ascertaining annual premiums on all policies involving risks on a single life. There remain still to be considered two special instances of the periodic premium, or two modifications of the annual premium, namely, premiums paid at intervals of less than one year, and premiums on policies which promise in the event of certain contingencies to return to the purchaser the premiums paid in without interest.