Accuracy of the Theory of Probabilities - The Law of Average

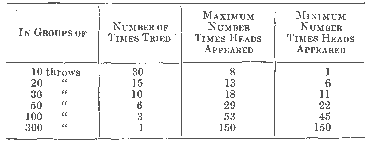
The accuracy of the theory of probabilities, on which future deaths will be estimated, or the closeness with which the theoretical approximates actual experience has important bearings on the success of any method of insuring lives. This accuracy depends on two factors: (1) the accuracy of the data, and (2) the number of units or trials taken. For instance, suppose that probabilities of death were computed on the basis of population statistics and death registration returns. Population censuses are taken by the Federal Government only once in ten years and these are supplemented in some states by a state enumeration in the year midway between two federal census years. Thus if death rates were to be computed for the year 1914 the last actual count of population would be for the year 1910, and the population for 1914 would have to be estimated. This estimate is certain to contain an element of error. Furthermore, the deaths among the estimated population would be determined from the registered deaths within the given area, but in no section of the United States are all deaths recorded. Indeed the qualification for admission into the "registration area" is the registration of only ninety percent, of the probable deaths. Therefore death rates based on population and death registration returns may contain two large elements of error and for this reason may fail to measure approximately the law of mortality. Mortality statistics, from whatever source, should be scrutinized searchingly in order to detect inaccuracies in the original data.

The second factor which determines the accuracy of the laws of probability is the number of units or trials taken. This may be illustrated by the coin example heretofore used, It was stated that the probability of falling heads up is ½. There is no inaccuracy in the data on which this fraction is based, for there are two sides only to the coin and one is heads. To illustrate the inaccuracy dependent on the number of trials, the following experiment was undertaken by the writer. An ordinary copper cent was flipped three hundred times and the results, whether heads or tails up, were recorded for each ten throws. If the probable experience had agreed absolutely with the actual, the results would have shown five throws heads and five throws tails for each ten trials. The actual results are recorded in the graph:

Results of Each 100 Trials in Groups of Ten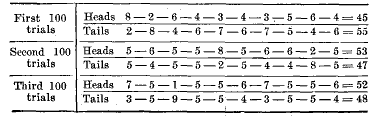

The table shows that in thirty trials of ten throws each the actual experience coincided with the probable in eleven cases, that in two instances heads appeared eight times out of ten, and in one case only once. These results in groups of ten may be combined into groups of twenty, thirty, fifty, one hundred, or in a single group of three hundred, and comparisons may then be made of the fluctuations in those respective groups. By this arrangement the original data assumes the form shown in the graph.

In the above table the data are arranged in fifteen groups of twenty throws each, ten groups of thirty, six of fifty, three of one hundred, and a single group of the three hundred throws and the number of times the coin fell heads or tails is shown for each group. The important fact to be considered is the relation between the probable and the actual experience in each grouping of the data. For instance, in twenty throws the probability is that heads will appear ten times, but the figures show that in one case this result occurred thirteen times and once Only six; in thirty throws heads appeared as many as eighteen times in two instances and as few as eleven the same number of times. The following brief table shows the maximum and the minimum number of times the coin turned heads up in any single trial of the specified number of throws:

If this data are now reduced to the form of percentage the results can be more readily compared, for the amount of the fluctuations will then have a common basis. It is understood that the probability of the coin falling heads up is ½ and this will be represented by fifty percent. The variation of the actual percentage from fifty percent, will therefore be the measure of the variation. The table presented herewith gives the results obtained:

This table furnishes the basis for an important generalization with reference to the accuracy of the theory of probability. It shows that where the coin was thrown ten times the results varied from a minimum of ten percent, to a maximum of eighty percent.; where twenty throws were made the variation was less, viz, from thirty to sixty-five percent; and that as the number of throws increased the variation became smaller and smaller and the percentage of times heads appeared approached fifty, the true probable percentage. That the three hundred throws resulted in exactly one hundred and fifty heads must be regarded as an accident; but it can be said with equal certainty that it would be impossible out of any three hundred purely chance throws to get as many as eighty percent, or as few as ten percent, to fall heads up. The generalization referred to above is as follows: Actual experience may show a variation from the true "probable" experience but as the number of trials is increased this variation decreases; and if a very great number of trials were taken the actual and the probable experience would coincide. Concretely, if the coin were flipped ten million times and it were a pure chance which way it would fall, the actual results would be so near five million times heads that the difference would be negligible. This generalization is called the law of average. This law is fundamental to all insurance. Premium rates are based on probable losses and will not accurately measure the risk unless the actual experience approximates the probable. That this approximation shall be realized it is at all times necessary to deal with a sufficiently large number of cases to guarantee that great fluctuations in results will be eliminated, i.e. to insure the operation of the law of average. In other words prediction of the future in life insurance based on what has happened in the past can be made for a large group of persons; it cannot be made for a single individual. When a mortality table shows that persons of a certain age die at the rate of seven per thousand per year that does not mean that out of a group of one thousand exactly seven will die within a year, but that out of a large group, maybe containing many thousands, the deaths will occur at the rate of seven per thousand.

With reference to the prediction of future mortality rates the law of average has a double application. Future mortality will be measured on the basis of past mortality data. These data of the past will supposedly be an approximate measure of the law of mortality heretofore referred to. But the statistics used for this purpose must be of sufficiently general application and must include a sufficiently large group of individuals to insure the operation of the law of average. Only in case this is so will the data in question be a fair measure of the true law of mortality. Granted then that the collected data are approximately correct, they become a measure of future mortality, only in case the group among whom the probable deaths are to be estimated is large enough to guarantee an average death rate or the operation of the law of average within the group.