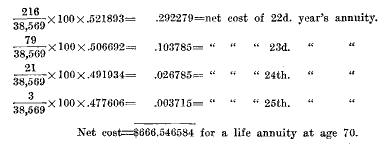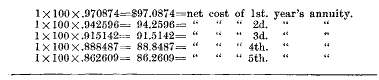Annuities

The remaining class of contracts to be analyzed are known as annuities. Annuities promise to pay the possessor a stated income, usually at intervals of one year during the lifetime of said person. It will be seen, therefore, that they furnish a type of investment whereby the recipient whose sole dependence is upon invested capital, can be assured of an income for life. And since the income is payable only during the life of the one person, the annuitant, a single annuity on one life does not furnish group protection, but each life must necessarily be covered by a separate contract.

Annuities covering a single life are of two kinds, immediate and deferred. Immediate annuities, sometimes referred to as the ordinary life form, may be temporary, i.e. limited to a term of years, may continue for the whole of life, or may promise a certain number of payments irrespective of the question whether the recipient be living or not. The latter contracts are sometimes spoken of as guaranteed annuities or annuities with a guaranteed minimum number of payments. The cost of each of these contracts will be considered in turn.

An immediate temporary annuity of $100 purchased, say, at age 70 and continuing for a period of ten years, will promise to pay the annuitant one hundred dollars one year from date of purchase if then living, and one hundred dollars at each anniversary of that date if still living until ten payments have been made. The cost of this contract will be the sum of money paid at the time of purchase, namely age 70, which will furnish these annual payments, and the net cost, which it is proposed here to determine, will be the amount necessary to provide merely for the payments of the sums promised to the annuitant without assessing against the contract anything for expenses. The formula used in computing net single premiums on insurances can again be used here, namely, net cost will equal the risk or probability insured against multiplied by the sum insured (the amount of the annuity) multiplied by the value of $1.00 discounted for the time the money is held. Since therefore a payment is made to the annuitant, if surviving, at the end of each year, the cost for each year must be determined separately and these sums added to obtain the total cost. The probability insured against is the probability that the annuitant will survive through the first year, through the second year, the third year, etc. It will be seen therefore that the annuity under consideration is equivalent to a series of ten pure endowments, one maturing in one year from date of purchase, one in two years, one in three years, etc., until ten have been paid. The probability that the first annuity payment will be made, if determined from the American Experience table, will equal the probability that a man aged 70 will survive one year, or expressed in the form of a fraction, 36178/38569. The $100. paid in case of survival is paid one year from the date of purchase of the annuity and therefore the net cost of the first payment will be the value of this sum discounted for one year at 3 percent, and multiplied by the probability of survival. Thus the total operation for the first year is as follows: 36178/38569 x 100 x. 970874 = $91.07 = net cost of first annuity payment.

In like manner the net cost for the remaining nine payments will be found by multiplying the probability of surviving through two, three, four years, etc., by the amount of the annuity of $100, discounted respectively, two, three, four years, etc. The entire computation for the ten years is as follows:

The temporary annuity at age 70, therefore, will cost net, $568.94, which sum is composed of the net costs of each of the separate yearly payments.

If the contract issued at age 70 promises to pay an annuity for the whole of life the computations must continue until the life surely fails and this occurs, according to the American Experience table, during the ninety-fifth year. The net cost of a whole-life annuity, or an ordinary life annuity as it is usually called, will, therefore, equal the net cost of a series of pure endowments, the first maturing at age 71 and the last at age 95, since all lives are assumed by the table to have surely failed before the beginning of the ninety-sixth year. The computation of the cost of this annuity is as follows, the first ten years being the same as for the term annuity just computed :

This sum of $666.55 therefore represents the net amount which, paid at age 70, will enable the insurance company to pay $100 per year to the annuitant during life.

If this same annuity guaranteed that the first five payments were to be certain, i.e. not affected by the death of the beneficiary before their completion, this fact would have to be taken into consideration in computing the net cost. The distinction would lie in the fact that these five payments would not be affected by death, or to put it in actuarial terms, the risk would equal certainty or one. The net cost of the first five payments would therefore be:

Total cost of annuity certain = $457.9708.

All payments following and including the sixth would be dependent on the probability of survival and their net cost would therefore be computed in the same manner as in the previous problem.